平均からのばらつきを数値にするために、分散という考え方を使いました。それと同じように、観測度数と期待度数のずれを数値にすることはできないのでしょうか。それを考えていきましょう。
まず、観測度数と期待度数のずれですから、それらをすべて足してみます。
ずれ案1=(観測度数−期待度数)の総和
しかし、これで実際に計算してみると、
(435-420)+(165-180)+(265-280)+(135-120)
=15+(-15)+(-15)+15
=0
となり、常に0になってしまいます。プラスのところとマイナスのところが打ち消し合っているからです。
そこで、分散の計算の時のように2乗してから足していきます。
ずれ案2=((観測度数−期待度数)の2乗)の総和
(435-420)^2+(165-180)^2+(265-280)^2+(135-120)^2
=15^2+(-15)^2+(-15)^2+15^2
=900
となり、よさそうです。
しかし、これでもまだまずいところがあります。たとえば、ポテトとチキンの売り上げデータを10日分とったとします。単純に考えて、データが1日分の10倍となったとすると、ずれの値は、
(4350-4200)^2+(1650-1800)^2+(2650-2800)^2+(1350-1200)^2
=150^2+(-150)^2+(-150)^2+150^2
=90000
となって、非常に大きくなってしまいます。
そこで、(観測度数−期待度数)の2乗を期待度数で割っておくことにします。
ずれ案3=(((観測度数−期待度数)の2乗)÷期待度数)の総和
(435-420)^2/420+(165-180)^2/180+(265-280)^2/280+(135-120)^2/120
=15^2/420+(-15)^2/180+(-15)^2/280+15^2/120
=0.536+1.250+0.804+1.875
=4.464
これをカイ2乗値と呼びます。カイというのは、ギリシャ文字で「χ」と書きます。
もう一度まとめておきます。
カイ2乗値=(((観測度数−期待度数)の2乗)÷期待度数)の総和
この式からわかることは、
ということです。
さて、計算した結果、カイ2乗値は4.464になりました。これはゼロではありませんから、観測度数と期待度数にずれがあることを示しています。それでは、このカイ2乗値は大きいのでしょうか、それともとるにたらないものなのでしょうか?
これを決めるためには、カイ2乗値の性質、つまりカイ2乗分布を調べておく必要があります。
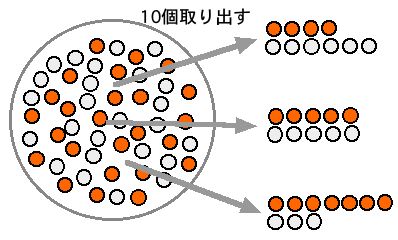
白とオレンジのピンポン玉をそれぞれ50個ずつ箱に入れておきます。よくかき混ぜて、無作為に10個取り出します。そのときの、白の数とオレンジの数を調べます。調べたら、また取り出した分を箱の中に戻して、また同じように無作為に10個取り出します。

このような実験を何回も繰り返すとどうなるでしょうか。
白とオレンジがそれぞれ5個ずつである場合は、比較的起こりやすそうです。もともと箱の中には半々ではいっていたのですから。
このときのカイ2乗値は(期待度数は5個と5個ですから)、
カイ2乗値=(5-5)^2/5+(5-5)^2/5=0
このようにゼロになります。
それでは、白とオレンジが、6個と4個になる場合はあるでしょうか。これも、よく起こりそうです。このときのカイ2乗値は、
カイ2乗値=(6-5)^2/5+(4-5)^2/5=0.4
0.4になります。
それでは、白とオレンジが、7個と3個になる場合はどうでしょう。6個と4個よりは起こりにくそうです。
カイ2乗値=(7-5)^2/5+(3-5)^2/5=1.6
1.6になりました。
さらに、白とオレンジが、8個と2個の場合はどうでしょうか。これはあまり起こらない場合です。
カイ2乗値=(8-5)^2/5+(2-5)^2/5=3.6
カイ2乗値は3.6になります。
最後に、白とオレンジが、9個と1個の場合はどうでしょう。これはめったに起こらない場合です。
カイ2乗値=(9-5)^2/5+(1-5)^2/5=6.4
カイ2乗値は6.4になりました。
以上のことを表にまとめると、次のようになります。
| 白とオレンジの個数 | 起こりやすさ(確率) | カイ2乗値 |
|---|---|---|
|
5個と5個
|
最も起こりやすい
|
0
|
|
6個と4個
|
起こりやすい
|
0.4
|
|
7個と3個
|
起こりにくい
|
1.6
|
|
8個と2個
|
かなり起こりにくい
|
3.6
|
|
9個と1個
|
非常に起こりにくい
|
6.4
|
起こりやすさ(確率)が小さくなればなるほど、カイ2乗値が大きくなっていることがわかります。
横軸にカイ2乗値を取り、縦軸に確率密度を取ると、次のようなカイ2乗分布が描けます。
確率密度というのは、たとえば横軸3のところで切った右側の面積が「カイ2乗値が3以上になる確率」になるように決めたものです。
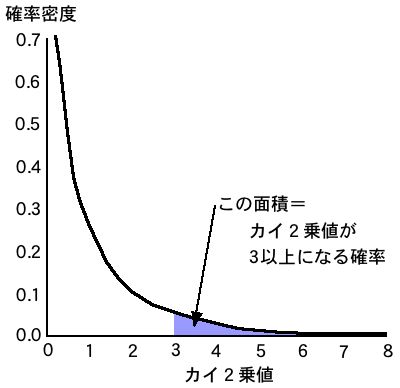
これを見ると、カイ2乗値がゼロに近づくほど、急激に確率が大きくなっていくことかわかります。逆にカイ2乗値が大きくなると、確率は非常に小さくなることがわかります。
この例では、白とオレンジのピンポン玉が50個と50個で半々になっていましたが、これがたとえば60個と40個であっても、カイ2乗値を計算して分布を描くと、同じカイ2乗分布になります。
また、この例では、取り出す個数は10個でしたが、これが20個でも、30個でも、カイ2乗値を計算して分布を描くと、同じカイ2乗分布になります。
このことから、カイ2乗分布がさまざまな場合に適用できることがわかります。
白とオレンジのピンポン玉を10個取ってくる場合は、白の数が決まれば、オレンジの数は自動的に決まります。つまり2種類の数のうち、自由に動かせるのは、そのうちひとつだけです。この数を「自由度」と呼びます。2種類のピンポン玉を取ってくる場合は、2−1で「自由度1」となります。
それでは、白とオレンジと青の3種類のピンポン玉ではどうでしょうか。この場合は、白とオレンジの数が決まると自動的に青の数が決まります。したがって、自由度は、3−1で2となります。
取り出す元の個数の割合が変わっても、また取り出す個数が変わっても、カイ2乗分布は変わりません。しかし、自由度が変わると、カイ2乗分布は変わります。図3.2のカイ2乗分布は、自由度1の場合の分布です。
自由度が変わると、次の図のようにカイ2乗分布も変わっていきます。
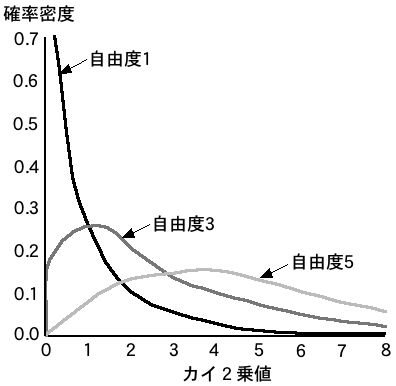
それでは、このカイ2乗分布を使って、ポテトとチキンの売り上げの割合に違いがあるかどうかを考えていきましょう。