

さて、因子負荷ということを説明した。共通因子が、観測変数に対してどれくらいの重み付けを持っているかということだ。
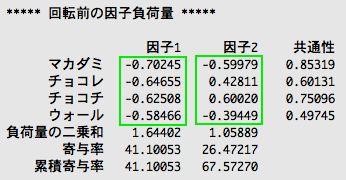
これだね。でもこのままだと、因子1、因子2とも「何の共通因子」かということがわかりにくい。
でも、試しにこれをグラフに表現してみよう。
横軸に因子1の因子負荷をとり、縦軸に因子2の因子負荷をとって、それぞれの観測変数をプロットしてみる。すると、こうなる。
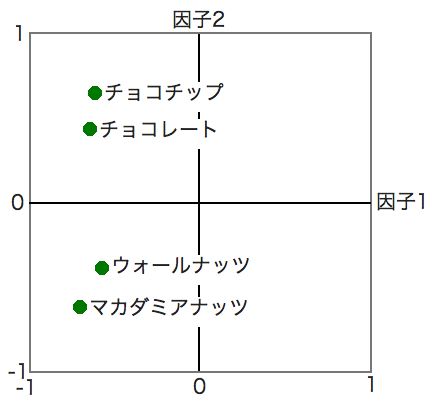
───あれっ! グラフにプロットしてみると、ちゃんとチョコ系はチョコ系にまとまっているし、ナッツ系はナッツ系でまとまっているわ。

そうなんだ。因子負荷をグラフにプロットしてみると、ちゃんと観測変数の地図ができていることがわかる。
問題は、このままだと、因子1、因子2といった共通因子の解釈が難しいということだ。
───解釈が難しいというのはどういうことなんですか?
簡単に言えば、名前がつけにくいということだね。できれば、因子1に「ナッツ系の因子」とか、因子2に「チョコ系の因子」というような名前をつけたい。そうすると解釈が簡単になるでしょう?
───なるほど、そうするにはどうしたらいいのですか?
軸を回転させることだ。こんなふうにね。
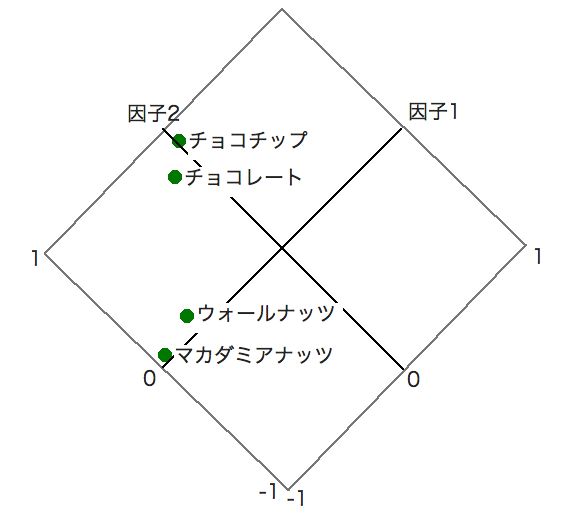
これは元の軸を、反時計回りに45度くらい回転してみたものだ。
そうするとどうだろう。因子1の軸は「ナッツ系の軸」にならないだろうか。そして、因子2の軸は「チョコ系の軸」に。
───ああ、ほんとうですね。確かに軸を回転させると解釈が簡単にできるようになります。
───でも、軸を勝手に回転してしまっていいんですか?
うん。いいんだ。元の観測変数同士の関係が変わらなければ、軸は自由にとることができるのさ。軸の回転方法にはいくつかのやり方があるが、ここでは「バリマックス法」という回転方法を使うことにしよう。
そうして、軸を回転させると、このような計算結果が出てくる。
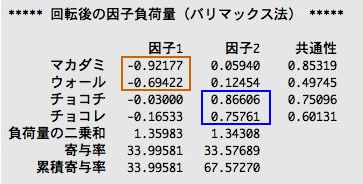
これを見てみると、因子1では、マカダミアナッツとウォールナッツが(マイナスだけど)高い値を示して、チョコレートとチョコチップはゼロに近い値になっているね。
一方、因子2では、マカダミアナッツとウォールナッツがゼロに近い値になっていて、チョコレートとチョコチップは正の高い値を示している。
こうなれば、因子1は「ナッツ系の因子」、因子2は「チョコ系の因子」と名前を付けることができる。
最終的な地図(因子負荷)はこんなグラフになるよ。

これで、ひとまずの因子分析はおしまいだ。

───きれいな地図にたどりついたわ。因子分析って、まるで探偵をしているみたいで、面白いわね。
───よし、それじゃ、元のデータを使って、因子分析をしてみよう。コーンも手伝って。

次は通過テストです。
(C) 2003 KogoLab