

固有値についてわかったところで、次に進もう。
次に、因子負荷(あるいは因子負荷量)というものが計算される。
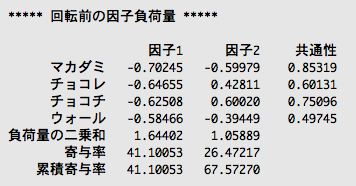
因子負荷というのは、観測変数に対して共通因子がどれくらいの強さで影響を与えているかを示したものだ。図にするとこうなる。
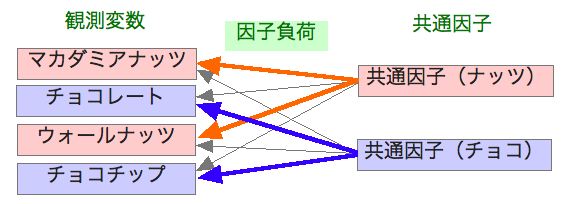
ナッツの共通因子は、マカダミアナッツとウォールナッツに大きな因子負荷があり(オレンジの矢印)、チョコレートとチョコチップに対する因子負荷は小さい(グレーの矢印)ということだ。
また、チョコの共通因子は、チョコレートとチョコチップに大きな因子負荷があり(ブルーの矢印)、マカダミアナッツとウォールナッツに対する因子負荷は小さい(グレーの矢印)ということだ。
───でも、三ヶ島先輩、おかしいですよ! 「因子1」の因子負荷を見てみると、4種類の観測変数すべてに対して、-0.5〜-0.7くらいの因子負荷になっているじゃないですか。
───その一方で、「因子2」の因子負荷を見てみると、チョコレートとチョコチップでは、0.4〜0.6、マカダミアナッツとウォールナッツでは、-0.4〜-0.6くらいなので、これは「チョコの共通因子」かなとは思うんですが。
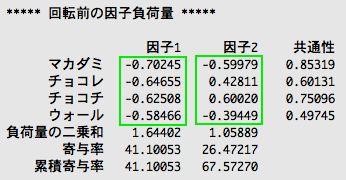
そう、確かに、因子1は4種類のすべてのアイスクリームに対して、同じような因子負荷の値を示している。これでは、因子1は何の因子かわからない。あえていえば、全部の観測変数に共通の共通因子ということになるけど。
一方、因子2については、ナッツの2種類には負の因子負荷量を示し、チョコの2種類には正の因子負荷量を示したということで、単純に「チョコの共通因子」とは呼べなくなる。あえていえば「チョコには正、ナッツには負の因子負荷を示す共通因子」ということだけど、これじゃわかりにくいよね。
これについては、次のセクションで解決していくことにしよう。

さて、次にいく前に、ここの結果で出ている、共通性や寄与率といったことについて説明しておこう。
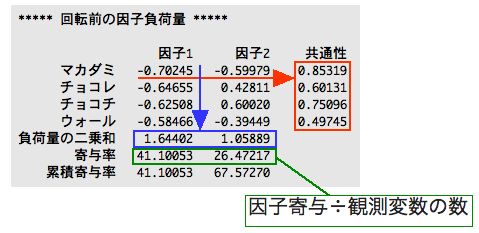
まず、共通性だ。これは観測変数ごとの因子負荷の2乗和だ。これが大きくなると、ここで採用した共通因子で説明される割合が大きくなるということになる。逆に、小さくなると、共通因子で説明される割合が小さくなる。これは、その観測変数が独自に持っている因子「独自因子」が効いているということになる。
もし、共通性が小さい観測変数があるとしたら、これは共通因子で説明される割合が小さいということだから、その因子分析の因子では説明しきれない変数である可能性が高い。そのような場合には、その変数を削除して再度、因子分析をしたりすることもある。いずれにしても、共通性の小さい変数には注意が必要だ。
次に、負荷量の2乗和で、これは因子寄与とも呼ばれる。これは因子ごとの因子負荷の2乗和で計算される。これは、その因子が全部の観測変数に対してどれくらいの寄与をしているかという指標になる。
因子寄与は、因子ごとに計算されて、その合計は理論的には観測変数の数になる。この場合だと、観測変数が4つなので、因子寄与の合計は4になる。そこで、因子寄与を観測変数の数で割ったものを寄与率と呼ぶ。単位はパーセントだ。寄与率を見れば、その因子が全体に対してどれくらい寄与しているのかが読み取れる。
累積寄与率というのは、寄与率を順次合計していったものだ。因子2までの累積寄与率は41.10053と26.47217を足し算したものになっているね。
(C) 2003 KogoLab