さて、標本の平均は49.2本になりました。問題は、この値を母集団の平均とみなしていいかどうかです。たくさんある母集団の中から、たった10個だけ取り出してきた標本の平均を、母集団の平均とみなしていいのでしょうか。
これを考えるには、母集団の平均・分散と標本の平均・分散との間にどのような関係があるのかを知っておく必要があります。
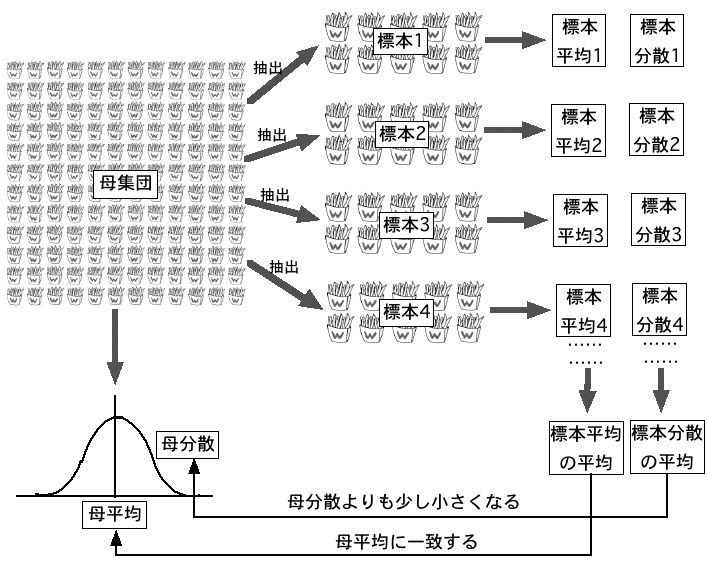
今、ポテトの母集団を考えて、そこから10個のデータを標本を抽出することを何回も繰り返したとしましょう。
10個のデータを無作為に抽出し、その平均と分散を計算します。それを標本平均1、標本分散1としておきます。次に、また別の10個のデータを無作為に抽出して、平均と分散を計算します。それを標本平均2、標本分散2としておきます。このようなことを何回も繰り返すわけです。
そうして得られた標本平均を平均すると、母集団の平均(母平均と呼びます)に等しくなります。そうなると、標本分散全体の平均も、母集団の分散(母分散と呼びます)に等しくなりそうな気がします。しかし、これは母分散よりも少し小さな値になります。
そこで、母分散の推定値として次のようなものを考えます。

不偏分散=((データ−平均値)の二乗)の総和÷(個数-1)
これは以前に出てきた分散の式で、「個数」の部分を「個数-1」にしたものです。これを「不偏分散」と呼びます。この不偏分散を「母分散の推定値」として使います。 まとめると次のようになります。
母集団全体の平均(母平均)と分散(母分散)を知りたいときに、母集団全部のデータは手に入らないことがほとんどです。そこで、母集団から無作為抽出をして標本のデータを手に入れます。そうすると標本の平均値は母平均の推定値として使えます。また、標本の不偏分散は母分散の推定値として使えます。
◇
それでは前に取った10個の標本データをもとにして、母集団の平均と分散を推定してみましょう。
表 ワクワクバーガーのポテトの本数(サンプルサイズ=10)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
47 |
51 |
49 |
50 |
49 |
46 |
51 |
48 |
52 |
49 |
私の計算では、平均値は49.2、不偏分散は3.51となりました。
不偏分散=31.6÷(10-1)=3.511111…
この結果から、母平均の推定値は49.2、母分散の推定値は3.51ということになります。あなたが買ったポテトの本数は49本だったので、平均的なポテトだということができるでしょう。
さて、標本から、ポテトの本数の推定値は49.2本であることを計算したあなたは店員さんに報告しました。

「店員さん、10個のデータからこのお店のポテトの本数の平均を推定すると、49.2本になりました。私が買ったポテトの本数は49本でしたので、これはまあまあ平均的なポテトだということができますね。」
「へえええ。全部のポテトの本数を調べなくても、その平均値がわかるんだ。すごいねえ、統計学ってのは。」
「平均値だけでなくて分散も推定できるんですよ。」
「なんだい? 分散ってのは?」
「ええと、その、つまり、データのばらつきのことです。」
「ふうん。しかし、全体のポテトのから見れば、たった10個のポテトのデータなのに、そこから全体の平均値がわかってしまうなんて、不思議だねえ。さっき、49.2本って言ったけど、それが全体のポテトの平均値にぴったり一致するわけじゃなんだろう?」
「『ぴったり一致』か。そういわれればそうですね。どうなんだろう?」