それでは「対応のあるt検定」をやっていきましょう。
それぞれの女子高生について、ワクワクバーガーの点数からモグモグバーガーの点数を引いて「点数の差」を計算します。
| 女子高生 | ワクワクバーガーの点数 | モグモグバーガーの点数 | 点数の差 |
|---|---|---|---|
| 1 | 90 | 95 | -5 |
| 2 | 75 | 80 | -5 |
| 3 | 75 | 80 | -5 |
| 4 | 75 | 80 | -5 |
| 5 | 80 | 75 | 5 |
| 6 | 65 | 75 | -10 |
| 7 | 75 | 80 | -5 |
| 8 | 80 | 85 | -5 |
| 平均 | 76.88 | 81.25 | -4.38 |
| 標本分散 | 43.36 | 35.94 | 15.23 |
点数の差は、平均が-4.38、標本分散が15.23となりました。つまりモグモグバーガーの方が4.38点だけ高い点数をもらったということになります。はたして、この点数の差は「意味のある差」なのかどうか。検定をします。
次のような指標tを考えます。
t=差の平均/差の標準誤差
標準誤差は、母分散を標本数で割り、その平方根をとったものでした。
差の標準誤差=sqrt(母分散/標本数)
ここで、母分散は不偏分散で推定しますので、
差の標準誤差=sqrt(不偏分散/標本数)
ところで、不偏分散は、平均からの偏差(平均からの差)の平方和を(標本数−1)で割ったものですから、
不偏分散/標本数=平均からの偏差の平方和/(標本数−1)/標本数
=平均からの偏差の平方和/標本数/(標本数−1)
=標本分散/(標本数−1)
となり、結局、次のようにも書けます。
差の標準誤差=sqrt(標本分散/(標本数−1))
最終的にtは、
t=平均の差/sqrt(不偏分散/標本数)
あるいは、
t=平均の差/sqrt(標本分散/(標本数−1))
となります。
それでは、実際にtを計算してみましょう(ここでは、途中結果も小数第2位で丸めていますが、実際には途中の計算は最大精度でしてください)。
まず、差の平均は、
差の平均=-4.38
次に、差の標準誤差を求めます。
差の標準誤差=sqrt((標本分散15.23/(標本数8−1))
=sqrt(15.23/7)
=1.48
あるいは、不偏分散が17.41(標本分散15.23よりも少し大きい)ですので、これを使って、
差の標準誤差=sqrt(不偏分散17.41/標本数8)
=sqrt(17.41/8)
=1.48
そうすると、tはこうなります。
t=-4.38/1.48 =-2.97
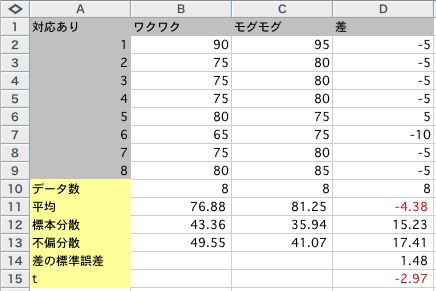
Excelで計算してみましょう。
ここでは、次のような関数を使っています。

さて、t=-2.97となりました。この値はどのくらいの確率で起こるのでしょうか。
それを調べるために、おなじみのt分布表を使いましょう。ここで、自由度は、差の標本数8から1をひいたもの、つまり7になります。
それでは、t分布表の自由度7のところを見てください。
t分布表
| 自由度 |
有意水準5% |
有意水準1% |
1 |
12.706 |
63.657 |
2 |
4.303 |
9.925 |
3 |
3.182 |
5.841 |
4 |
2.776 |
4.604 |
5 |
2.571 |
4.032 |
6 |
2.447 |
3.707 |
7 |
2.365 |
3.499 |
8 |
2.306 |
3.355 |
9 |
2.262 |
3.250 |
10 |
2.226 |
3.169 |
| 11 |
2.201 |
3.106 |
| 12 |
2.179 |
3.055 |
| 13 |
2.160 |
3.021 |
| 14 |
2.145 |
2.977 |
| 15 |
2.131 |
2.947 |
| 16 |
2.120 |
2.921 |
| 17 |
2.110 |
2.898 |
| 18 |
2.101 |
2.878 |
| 19 |
2.093 |
2.861 |
| 20 |
2.086 |
2.845 |
21 |
2.080 |
2.831 |
22 |
2.074 |
2.819 |
23 |
2.069 |
2.807 |
24 |
2.064 |
2.797 |
25 |
2.060 |
2.787 |
26 |
2.056 |
2.779 |
27 |
2.052 |
2.771 |
28 |
2.048 |
2.763 |
29 |
2.045 |
2.756 |
| 30 |
2.042 |
2.750 |
| 40 |
2.021 |
2.704 |
| 60 |
2.000 |
2.660 |
| 120 |
1.980 |
2.617 |
| ∞ |
1.960 |
2.576 |
自由度7において、有意水準5%のtは2.365、有意水準1%のtは3.499と書いてあります。
いま、有意水準を5%に設定します。
さて、計算したtは、-2.97でしたので、5%有意水準での棄却域に入りました。したがって帰無仮説は棄却されます。結論としては、ワクワクとモグモグの評価点の平均には差があるということになります。
さて、上でやった対応のあるt検定の結論は、4.38点の差について「ワクワクとモグモグの評価点の平均には差がある」ということになりました。
しかし、前の章でやった対応のないt検定の結論は、それより大きい5.00点の差があったのに「差がない」というものでした。
これはどういうことなのでしょうか。
対応のあるt検定では、同一個人内でデータを取るため、差の標準誤差が小さくなります。一方、対応のないt検定では、個人間でデータを取るため、個人差が大きくなり、差の標準誤差が大きくなります。
標準誤差が小さくなるということは、信頼区間の幅が狭くなり、それだけ確実に真の値を推測できるということです。
したがって、対応のあるt検定では、有意差を見いだす検出力が大きくなります。
これが、対応のあるt検定では、対応のないt検定よりも、差が小さかったのに「有意な差(意味のある差)」を見いだすことができた理由です。